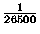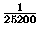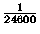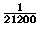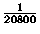Brescia, 17 dicembre 2005
Allenamenti di Matematica
Problemi di Logica, Probabilità e Combinatoria
- Cinque amici hanno
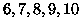 anni; qual è la probabilità
che scelti due di essi a caso la differenza delle loro età
sia almeno
anni; qual è la probabilità
che scelti due di essi a caso la differenza delle loro età
sia almeno 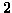 anni? Si supponga che le scelte siano equiprobabili
ed indipendenti l'una dall'altra.
anni? Si supponga che le scelte siano equiprobabili
ed indipendenti l'una dall'altra.
- La famiglia Petersen ha
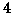 figli. Il più giovane è un maschio,
così come almeno uno degli altri
figli. Il più giovane è un maschio,
così come almeno uno degli altri 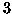 . Qual è la probabilità
che il figlio più vecchio sia una femmina?
. Qual è la probabilità
che il figlio più vecchio sia una femmina?
- Una gara di matematica è composta da
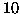 domande a risposta
multipla, ciascuna con quattro possibili risposte contrassegnate
dalle lettere
domande a risposta
multipla, ciascuna con quattro possibili risposte contrassegnate
dalle lettere 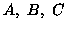 e
e 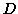 (per ogni domanda vi è una e
una sola risposta corretta). Carlo viene a sapere che la lista
delle risposte corrette contiene tre lettere
(per ogni domanda vi è una e
una sola risposta corretta). Carlo viene a sapere che la lista
delle risposte corrette contiene tre lettere 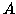 , tre lettere
, tre lettere
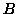 , due lettere
, due lettere 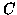 e due lettere
e due lettere 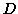 . Qual è la probabilità
che Carlo, scegliendo a caso una lista che abbia questa
caratteristica, risponda correttamente a tutte le domande?
. Qual è la probabilità
che Carlo, scegliendo a caso una lista che abbia questa
caratteristica, risponda correttamente a tutte le domande?
- (a)
-
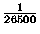
- (b)
-
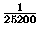
- (c)
-
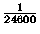
- (d)
-
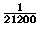
- (e)
-
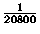
- Nicola e Gianmarco hanno una scatola con dentro
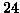 carte, di cui
carte, di cui
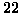 nere e
nere e 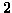 rosse. Nicola punta su un numero
rosse. Nicola punta su un numero 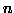 tra
tra 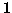 e
e
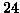 , dopo di che Gianmarco inizia a pescare
, dopo di che Gianmarco inizia a pescare 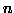 carte,
sfogliandole una ad una. Nicola vince se la carta numero
carte,
sfogliandole una ad una. Nicola vince se la carta numero 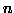 è
la prima carta rossa che esce. Su quale numero gli conviene puntare
per avere la massima probabilità di vittoria?
è
la prima carta rossa che esce. Su quale numero gli conviene puntare
per avere la massima probabilità di vittoria?
- Sono date
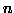 cifre, nessuna delle quali
cifre, nessuna delle quali 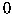 , generate in modo casuale
e indipendente. Trovare la probabilità che il loro prodotto sia
divisibile per
, generate in modo casuale
e indipendente. Trovare la probabilità che il loro prodotto sia
divisibile per 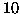 .
.
- Si scelgano a caso tre vertici di un poligono regolare di
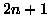 lati. Trovare la probabilità che il centro del poligono
si trovi dentro il triangolo risultante.
lati. Trovare la probabilità che il centro del poligono
si trovi dentro il triangolo risultante.
- Se si scelgono sequenzialmente a caso
sei punti sulla circonferenza di un cerchio, qual è la
probabilità che il triangolo formato dai primi tre sia
disgiunto da quello formato dai tre successivi?
-
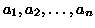 è una successione arbitraria di interi
positivi. Si prende a caso un elemento della successione. Il suo
valore è
è una successione arbitraria di interi
positivi. Si prende a caso un elemento della successione. Il suo
valore è 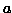 . Si prende a caso un altro elemento,
indipendentemente dal primo. Il suo valore è
. Si prende a caso un altro elemento,
indipendentemente dal primo. Il suo valore è 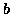 . Poi un terzo,
di valore
. Poi un terzo,
di valore 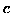 . Dimostrare che la probabilità che
. Dimostrare che la probabilità che 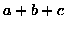 sia
divisibile per
sia
divisibile per 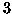 è almeno
è almeno 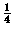 .
.
- Si lancia ripetutamente un dado.
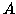 vince se esce
vince se esce 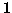 o
o 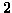 in due
lanci consecutivi,
in due
lanci consecutivi, 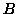 vince se esce
vince se esce
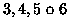 in due lanci
consecutivi. Trovare la probabilità di vittoria di ciascun
giocatore se il dado è lanciato al più
in due lanci
consecutivi. Trovare la probabilità di vittoria di ciascun
giocatore se il dado è lanciato al più 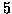 volte.
volte.
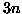 studenti sono seduti in
studenti sono seduti in 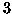 file da
file da 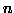 . Gli studenti se ne
vanno uno alla volta. Tutti gli ordini in cui se ne vanno sono
equiprobabili. Trovare la probabilità che non ci siano mai due
file in cui il numero degli studenti rimanenti differisce di due
o più studenti.
. Gli studenti se ne
vanno uno alla volta. Tutti gli ordini in cui se ne vanno sono
equiprobabili. Trovare la probabilità che non ci siano mai due
file in cui il numero degli studenti rimanenti differisce di due
o più studenti.
- Nell'isola dei furfanti e dei cavalieri, gli abitanti si dividono in
due categorie: i furfanti che mentono sempre, e i cavalieri che
dicono sempre la verità. Quando furono annunciate le elezioni
presidenziali c'erano
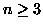 candidati, tutti autoctoni. Durante
un dibattito televisivo tutti i candidati, a turno, si presentarono.
Il
candidati, tutti autoctoni. Durante
un dibattito televisivo tutti i candidati, a turno, si presentarono.
Il 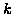 -esimo candidato disse: ``Tra tutti i candidati, me escluso,
ci sono
-esimo candidato disse: ``Tra tutti i candidati, me escluso,
ci sono 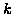 furanti più che cavalieri''.
furanti più che cavalieri''.
Quanti candidati c'erano?
- Cinque animali (
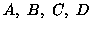 ed
ed 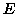 ) sono o cani o lupi. I cani
dicono sempre la verità, mentre i lupi mentono sempre.
) sono o cani o lupi. I cani
dicono sempre la verità, mentre i lupi mentono sempre. 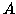 dice
che
dice
che 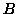 è un cane.
è un cane. 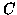 dice che
dice che 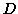 è un lupo.
è un lupo. 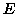 dice che
dice che 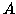 è un cane.
è un cane. 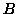 dice che
dice che 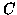 è un lupo.
è un lupo. 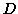 dice che
dice che 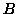 ed
ed 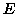 sono animali diversi. Quanti lupi ci sono nel gruppo dei cinque
animali?
sono animali diversi. Quanti lupi ci sono nel gruppo dei cinque
animali?
- Una stanza rettangolare ha le pareti rivolte nelle direzioni dei
quattro punti cardinali e ci sono quattro porte d'accesso. Tre
persone si trovano nella stanza e fanno le seguenti affermazioni.
Prima persona: ``Non ci sono porte sulla parete Sud''. Seconda
persona: ``Ci sono porte solo sulla parete Nord''. Terza persona:
``Su ogni parete c'è al massimo una porta''. Che cosa si può
dire per certo delle affermazioni fatte?
- (a)
- L'affermazione fatta dalla prima persona è vera,
- (b)
- l'affermazione fatta dalla seconda persona è vera,
- (c)
- l'affermazione fatta dalla terza persona è vera,
- (d)
- almeno una affermazione è falsa,
- (e)
- non si può dire niente di certo sulle affermazioni fatte.
- Quattro bambine, Alice, Bianca, Cecilia e Daniela, decidono di
comprare un palloncino a testa da un venditore che ha solo
palloncini rossi e blu. Compreranno il palloncino una dopo l'altra:
prima Alice, poi Bianca, poi Cecilia e infine Daniela. Bianca
dice: ``Se Alice lo comprerà rosso, anch'io lo comprerò
rosso''. Cecilia dice: ``Io lo comprerò dello stesso colore di
Bianca''. Daniela dice: ``Se Alice lo comprerà blu, io lo
comprerò dello stesso colore di Cecilia''. Quale delle seguenti
affermazioni è sicuramente vera?
- (a)
- È impossibile che quattro bambine comprino un palloncino
rosso,
- (b)
- almeno tre bambine compreranno un palloncino dello stesso
colore,
- (c)
- Daniela e Bianca compreranno un palloncino dello stesso
colore,
- (d)
- almeno due bambine compreranno un palloncino rosso,
- (e)
- nessuna delle precedenti affermazioni è sicuramente vera.
- Andrea e Alberto sono gemelli e si assomigliano in tutto tranne in
una cosa: uno di loro è bugiardo di lunedì, martedì e
mercoledì, mentre l'altro mente di giovedì, venerdì e sabato.
Negli altri giorni sono sinceri. Un certo giorno uno dice: ``Io
sabato dico bugie, e anche domenica''. L'altro risponde: ``Domani
dirò bugie''. In che giorno si è svolto il dialogo?
- Tra la popolazione dell'arcipelago del Disaccordo esistono solo due
cognomi: Delvero e Delfalso. Una tradizione ancestrale vuole che un
Delvero non menta mai, mentre un Delfalso non dice mai la verità.
Un navigatore fa un naufragio sull'arcipelago e incontra tre giovani
indigeni. Conoscendo la particolarità dell'isola, chiede ai suoi
interlocutori i loro cognomi. Ecco le risposte che ottiene:
Eric: ``Gli altri due si chiamano Delfalso''
Maria: ``Due di noi si chiamano Delfalso''
Stefano: ``Solo uno di noi si chiama Delfalso''
Quali sono i cognomi delle persone incontrate nel naufragio?
- Un viaggiatore si trova sull'arcipelago del Disaccordo per andare
ad una riunione nella più grande città del luogo. Purtroppo
ha ricevuto solo indicazioni sommarie, e trovandosi davanti ad un
bivio inaspettato non sa quale delle due direzioni prendere. La
città dove si deve dirigere è per fortuna molto famosa, e tutti
gli abitanti dell'arcipelago sanno dove si trova. Arrivano allora
da due direzioni opposte due abitanti del luogo. Il nostro
viaggiatore conosce le abitudini dell'arcipelago del Disaccordo
e sa che uno di essi (ma non sa quale) è un Delvero e l'altro un
Delfalso. Le leggi dell'arcipelago sono molto severe nei confronti
dei viaggiatori, ed è scritto che, per ottenere un'informazione,
si può porre una sola domanda, ad una sola persona. Cosa dovrà
quindi chiedere il nostro amico viaggiatore?
- Si gioca a Tennis.
In un torneo di tennis, solo i vincitori di ogni incontro giocano quello successivo; così fino alla proclamazione del vincitore del torneo.
Se i giocatori sono 128, quanti incontri devono essere giocati in tutto per proclamare il vincitore del torneo?
- Casalinghe confuse.
Tre paia di calzini, uno rosso, uno blu e uno verde, sono stesi in fila. Sapendo che due calzini dello stesso colore non sono vicini l' uno all' altro, quante successioni di colori si possono avere?
- Scrivi scrivi...
Su una striscia molto lunga sono scritte di seguito, in ordine alfabetico, tutte le parole di 4 lettere (incluse quelle prive di significato) ottenibili con le 21 lettere del nostro alfabeto a partiore da AAAA. Qual è la 2005-esima lettera scritta?
- La sala consigliare di Matelandia.
La sala consigliare della città di Matelandia è molto piccola: ci stanno solamente 10 seggiole contro i muri di tre lati della stanza (l'ingresso sul quarto lato) e un tavolo al centro. All'inizio di ogni riunione il sindaco entra per primo e i nove consiglieri entrano rigorosamente in ordine di età: dal più anziano al più giovane. Il sindaco sceglie dove sedersi, mentre ciascuno dei consiglieri, a causa delle ristrettezze del luogo, deve sedersi accanto a qualcuno che si è già sistemato. In quanti modi diversi può disporsi il consiglio?
- Consiglieri... maldisposti.
Proprio oggi è in corso il consiglio di amministrazione della principale banca della città, convocato d'urgenza a causa del furto subito la notte scorsa. I sei consiglieri arrivano trafelati alla riunione e si siedono a caso ai sei posti della tavola rotonda che troneggia al centro della sala riunioni. Ognuno dei sei consiglieri ha davanti a sé il segnaposto (mobile) che avrebbe dovuto indicargli dove sedersi. Visto il momento critico, decidono di restare tutti seduti al loro posto e di scambiarsi il segnaposto solo se due consiglieri seduti vicino hanno ciascuno il segnaposto dell' altro. Quante possono essere le diverse possibili distribuzioni dei segnaposto al termine di tutti gli scambi?
(Due distribuzioni di segnaposto che differiscono per una rotazione o per una qualsiasi trasformazione di simmetria del tavolo sono da considerarsi distinte.)
- Su due ruote.
Ad una gara a punti su pista partecipano nove concorrenti. Ad ogni traguardo intermedio vengono assegnati 9 punti al primo, 8 al secondo, 7 al terzo e così via fino ad assegnare 1 punto all'ultimo. Prima dell'ultimo sprint (in cui il punteggio vale doppio) la classifica vede al comando Abdujaparov con 2 punti di vantaggio su Boardman e 9 su Cipollini. Gli altri concorrenti hanno un distacco in punti tale da non consentire più loro di aggiudicarsi la gara.
Quanti sono i possibili diversi piazzamenti dei tre corridori nell' ultimo sprint che permettono a Cipollini di vincere la gara?
- Insiemi colorati.
Siano
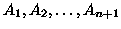 insiemi aventi ciascuno
insiemi aventi ciascuno 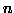 elementi, tali che ogni coppia di insiemi abbia esattamente un elemento in comune e che ogni elemento dell'unione appartenga ad esattamente due insiemi. Per quali valori di
elementi, tali che ogni coppia di insiemi abbia esattamente un elemento in comune e che ogni elemento dell'unione appartenga ad esattamente due insiemi. Per quali valori di 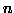 è possibile colorare con due colori gli elementi dell'unione in modo che ogni insieme possegga un ugual numero di elementi dei due colori?
è possibile colorare con due colori gli elementi dell'unione in modo che ogni insieme possegga un ugual numero di elementi dei due colori?
- Cubi e triangoli.
Dato un cubo
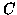 , quanti sono i triangoli che hanno per vertici tre vertici di
, quanti sono i triangoli che hanno per vertici tre vertici di 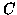 e che non giacciono su nessuna delle facce di
e che non giacciono su nessuna delle facce di 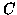 ?
?
- Per distinguere.
Le nuove targhe automobilistcihe sono costituite da due lettere, tre cifre e altre due lettere (scelte nell'alfabeto inglese di 26 lettere). Quante targhe al massimo si possono emettere se si vuole che due qualsiasi di esse differiscano in almeno due posizioni?
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_antialias_text lpc16dicOK.tex
The translation was initiated by DMF Web on 2005-12-21


DMF Web
2005-12-21