Disfida Matematica 2007
Soluzioni dei problemi 6 - 10
- 6.
- Finanziamenti occulti. Intanto osserviamo che il
numero di calzini per ogni colore è pari, quindi se si esaurisce
un colore non ne rimangono di spaiati. Poi, è necessario prendere
almeno 4014 calzini, per averne un paio a testa. Inoltre, poiché i
colori sono 6, il caso peggiore è che ``avanzino'' 6 calzini
spaiati, ovvero ne manchino 3 paia. Se ne prendo ancora 5 sono certo
di farne almeno altre 3 paia, che sono quelle che mancavano. Se
invece ne avessi presi ancora 4, avrebbero potuto essere due di un
colore e due di un altro, ovvero due paia già complete, e ne
sarebbe mancato ancora un paio. Quindi la risposta è
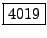 .
.
- 7.
- Exit polls. Denotando con
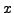 il numero degli elettori
che ha effettivamente votato ``Sì'', si ha ovviamente che il
numero di quelli che hanno dichiarato di aver votato ``Sì'' è
dato da
il numero degli elettori
che ha effettivamente votato ``Sì'', si ha ovviamente che il
numero di quelli che hanno dichiarato di aver votato ``Sì'' è
dato da 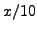 più
più
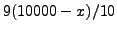 , dove chiaramente
, dove chiaramente 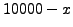 è
il numero degli elettori che hanno votato ``No''. Quindi
è
il numero degli elettori che hanno votato ``No''. Quindi
da cui
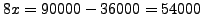 . La risposta è
quindi
. La risposta è
quindi 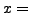
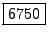 .
.
- 8.
- Tagli alla spesa.
L'equazione (logaritmica) che caratterizza
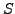 è
è
La soluzione è della forma 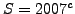 , per cui il
più grande fattore primo di
, per cui il
più grande fattore primo di 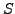 è più semplicemente il più
grande fattore primo di 2007. Una semplice scomposizione in fattori
dà la risposta
è più semplicemente il più
grande fattore primo di 2007. Una semplice scomposizione in fattori
dà la risposta
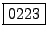 .
.
- 9.
- L'aiuola bipartisan.
Facciamo una figura tanto per chiarirci le idee.
Chiamiamo
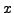 un angolo formato dalle due rette. Poiché
l'area del settore circolare di raggio
un angolo formato dalle due rette. Poiché
l'area del settore circolare di raggio 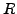 e angolo (in gradi
sessagesimali)
e angolo (in gradi
sessagesimali) 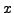 è
è
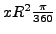 , si ha l'equazione
, si ha l'equazione
da cui segue
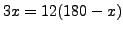 , ovvero
, ovvero 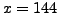 . L'altro angolo misura quindi
. L'altro angolo misura quindi
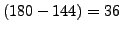 gradi. La risposta è
gradi. La risposta è
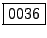 .
.
- 10.
- Panem et circenses. Cerchiamo intanto gli anni
giusti tra il 1900 e il 1999. Poiché la somma delle cifre di tali
anni è al massimo 28 (per il 1999) e la somma delle cifre delle
cifre è al massimo 10 (per 28 appunto, o anche per 19), la somma
totale da aggiungere all'anno è al massimo 38, quindi si può
partire almeno dall'anno
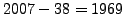 . Inoltre osserviamo che ogni
volta che si incrementa di un anno può succedere che incrementi di
tre il risultato finale, oppure diminuisca di 6 o di 15 (quando si
salta alla decina successiva, la somma delle cifre cala di 8).
Quindi, poiché 2007 è multiplo di 3, dobbiamo partire con un
multiplo di 3. Il primo è 1971, che dà 1998, dunque a
1974 che dà 1998, dunque a 1977 che dà 2007. Abbiamo
trovato il primo. Continuiamo con 1980, che dà ancora 2007. Ecco
il secondo. Arriviamo a 1983, che dà ancora 2007. Ecco il terzo.
L'anno 1986 dà invece 2016 (
. Inoltre osserviamo che ogni
volta che si incrementa di un anno può succedere che incrementi di
tre il risultato finale, oppure diminuisca di 6 o di 15 (quando si
salta alla decina successiva, la somma delle cifre cala di 8).
Quindi, poiché 2007 è multiplo di 3, dobbiamo partire con un
multiplo di 3. Il primo è 1971, che dà 1998, dunque a
1974 che dà 1998, dunque a 1977 che dà 2007. Abbiamo
trovato il primo. Continuiamo con 1980, che dà ancora 2007. Ecco
il secondo. Arriviamo a 1983, che dà ancora 2007. Ecco il terzo.
L'anno 1986 dà invece 2016 (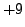 ), e sono sbagliati anche il 1989,
1992, 1995, 1998. Il 2001 è ancora giusto, e poi basta. Risultano
quindi quattro anni: 1977, 1980, 1983, 2001, la cui somma è
), e sono sbagliati anche il 1989,
1992, 1995, 1998. Il 2001 è ancora giusto, e poi basta. Risultano
quindi quattro anni: 1977, 1980, 1983, 2001, la cui somma è
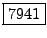 .
.
DMF Web
2007-04-19
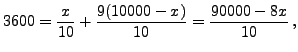
![\includegraphics[height=3cm]{aiuola}](img14.png)
![\begin{multline*}
\left[2x(1^2) + 2(180-x)(2^2-1^2) + 2x(3^2-2^2)\right]\frac{\p...
...(1^2) + 2x(2^2-1^2) +
2(180-x)(3^2-2^2)\right]\frac{\pi}{360}\,,
\end{multline*}](img17.png)
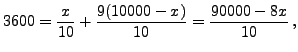
![\includegraphics[height=3cm]{aiuola}](img14.png)
![\begin{multline*}
\left[2x(1^2) + 2(180-x)(2^2-1^2) + 2x(3^2-2^2)\right]\frac{\p...
...(1^2) + 2x(2^2-1^2) +
2(180-x)(3^2-2^2)\right]\frac{\pi}{360}\,,
\end{multline*}](img17.png)